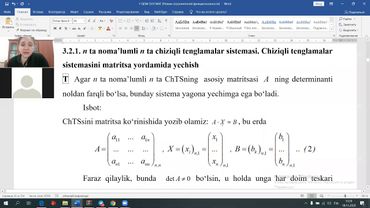
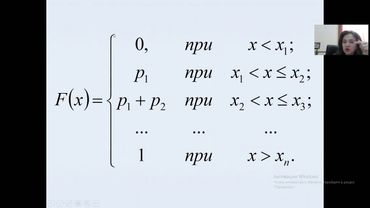Экономическая математика практика 4

Значит, начали практическую часть.

Ну, давайте начнем с Гмурмана, потом посмотрим несколько задач.

Вот, смотрите.

Читаю, 92-я задача.

В пирамиде 5 винтовок, ну, то есть 5 оружия, 3 из которых снабжены оптическим прицелом.

В пирамиде 5 винтовок, 3 из которых снабжены оптическим прицелом.

Вероятность того, что стрелок поразит мишень при выстреле из винтовки,

с оптическим прицелом равно 0,95.

Для винтовки без оптического прицела эта вероятность равно 0,70.

Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел на удачу из взятой винтовки.

Значит, смотрите.

Расписываем условия.

Сколько винтовок у меня?

Пять.

Правильно?

Доска видна, ребята?

Да, она видна.

Пять винтовок.

Теперь, из пяти сколько с оптическим?

Три.

Три у нее оптические, это снайперские, а два простых, согласны, да?

Без прицела.

Теперь,

Всего у меня пять винтов.

Что я должна найти?

Значит, стрелок приходит, он не знает, допустим, он не знает, выбирает любой из винтовок и стреляет.

Мне нужно найти вероятность события ААА, при котором, что стрелок

Попадет в мишень.

Вот основное мое событие, которое я должна найти.

Я должна найти ПА.

Теперь давайте рассмотрим гипотезы.

Какие могут быть предположения?

Какие винтовки лежат?

У меня два вида винтовки.

ПА1.

Стрелок.

Ну, мы с вами H обозначили.

Давайте H сделаем, чтобы вам было легче.

H1.

Стрелок выбрал с оптическим прицелом.

А второе что будет, ребята?

Стрелок.

Второй будет H2.

Простой.

Значит, стрелок выбрал простую винтовку.

Он же может простую тоже выбрать, правильно?

Теперь давайте найдем вероятности вот этих H1, H2.

PH1 чему равен, ребята?

Вот я пришла, я стрелок, например.

Выбираю любую винтовку.

Мне нужно найти вероятность, что из пяти винтовок я выберу со снайперским, то есть с прицелом.

Чему будет равна вероятность?

Три на пять?

Три на пять, правильно.

PH2, то есть приду и выберу простую винтовку, будет две пяток.

Все, у меня больше...

Больше гипотез, больше предположений быть не может, потому что у меня всего два вида винтовок.

Либо оптический, либо простой.

Теперь, что я должна найти?

Я должна найти... Я выбрала с оптическим прицелом и попала в мишень.

Вот я читаю, смотрите.

Я выбрал вероятность выбора простого

с оптическим прицелом винтовку, и попадание в мишень, вот попал в мишень, чему равно?

Это было задание.

0,95.

То есть стрелок попадет в мишень, если он будет стрелять со снайперски, это 0,95.

По заданию есть.

Если я выберу вторую винтовку, простую, и я попаду в цель, это у меня 0,75.

Я специально рядышком написала, ребята.

Ну и теперь нахожу.

ПА, чему у меня равен?

Вероятность гипотезы первой на условную вероятность события А при условии, что я уже выбрала снайперскую.

Плюс PH2, ребята.

А?

Вот, пожалуйста.

Теперь числа ставим и все.

То есть 3 пятых 0,6 на 0,95 плюс 0,4 на 0,7.

Равно... Посчитаете сами или посчитаете?

Так, это 0,28, 0,85.

0,95...

95 на 6 умножьте.

0, 3 в уме, 54, 58.

Вот.

Складываем 0, 28.

И правильно посчитала я?

0, 86.

Что получится?

0, 86.

Вопрос ясен?

Да.

Задача ясна, да?

Какой?

Вот этот дробь, что ли?

Почему?

Из 5, 3, ну, хочешь 0,6, сделай разницу, нет?

Можно.

Теперь давайте 94-я задача.

Очень популярная задача.

Я стираю, а у вас будет запись, ребята.

94-я задача.

Что она говорит?

В первой форме, это по Васю, но уже к Мурману.

Сейчас, секундочку, у меня доска вылетает.

Первые урни содержатся 10 шаров.

Из них 8 белых.

Вот я рисую урну.

8 белых, 2 черных.

Во второй урне 20 шаров, 4 белых.

Значит, 4 черных, ой, 16 черных, 4 белых.

Из каждой урны на удачу извлекли по одному шару.

Отсюда один шар, отсюда один шар.

Затем из этих двух шаров выбираем еще один шар.

Надо найти вероятность того, чтобы был вот этот шар последний белый.

Ну-ка, давайте подумайте.

Две минуты вам, время на то, чтобы вы размыслили.

Давайте теперь распишем основное событие.

Событие А. В чем заключается?

Вытащить белый шар.

Правильно, выбранный последний шар, то есть последний шар белый.

Теперь давайте рассмотрим гипотезы.

Какие могут быть гипотезы, ребята?

Предположения, какие могут быть?

Мне нужно предположение о составе вот этих двух.

Первое, B1.

H1, да, давайте.

Мы с вами H обозначали.

Давайте H обозначим.

H1.

Какой шар можем вытащить с первого?

Белый.

Со второго тоже можем мы белый вытащить?

Белый, белый.

Два белых может быть, да?

Может.

Теперь H2.

Какие шары могут быть?

Ну-ка.

Белый, черный.

Может быть такой?

H3.

Еще какой может быть?

Черный, белый.

Черный, белый.

И H4?

Черный, черный.

Все.

Других случаев быть не может.

Теперь давайте рассмотрим вероятность каждого из них.

Вот я поменьше написала, мне просто места не хватит.

Я хочу.

PH1.

Вероятность того, что я вытащу с первого белый шаг.

Чему равно?

Отсюда я вытащила белый.

Вот.

Эти два события, вот эти белые-белые, не зависят друг от друга.

Потому что у меня два ящика.

Да.

Восемь десятых.

Ноль восемь.

Правильно.

А со второго белой?

Ноль два.

Четыре двадцатых.

Правильно?

PH2.

Белый.

0,8.

0,8.

Черный со второго.

0,8.

Поняли, да?

Тоже 0,8.

PH3.

Черный.

0,2.

И белый.

0,4.

И PH3.

Черный 2 десятых.

И со второго тоже черный.

16 двадцатых.

Вы должны сложить вот эти вероятности.

Чему оно будет равно?

Оно должно быть равно единице.

Знаменатель у вас 200.

Считаем числители.

32, 64, 8.

Вот я пишу 32, 64, 8.

Так, и...

Тридцать два.

Будет двести, нет?

Шестьдесят четыре плюс шестьдесят четыре.

Где я ошиблась?

Вот это не шестьдесят четыре.

Это сколько будет?

Восемь на это сто двадцать восемь будет.

Так, сорок, сто шестьдесят восемь, тридцать два, да, двести.

Сумма будет равна единице.

Вы правильно посчитали.

Теперь мы должны найти условные вероятности.

Если я выберу из первого белый, со второго тоже белый, то есть H1.

Из этих двух я выберу один шар.

И он будет белый.

Чему будет равен, ребята?

Я уже ящики забываю.

Я смотрю уже сюда.

У меня в руках два белых шара.

Белый и белый.

Из этих двух я выбираю один шар.

И мне нужна вероятность того, что он будет белый.

Чего будет равен?

Одна вторая.

Почему?

Два белых.

Один.

У меня в руках два шара.

Оба белые.

Если я выберу...

С одного белый, с другого черный.

И выбор белого у меня будет, вот здесь будет одна вторая.

Потому что два шара, и здесь один только белый.

Здесь то же самое.

Выберу с первого черный, со второго белый.

То есть у меня один белый шар, тоже будет из двух один.

И последний, если у меня в руках два черных шара, выбор белого, вообще не повезло.

Чему будет это равно?

Нулю.

Ну, 0 вторых, потому что.

Вот теперь соответствующие вероятности умножаю.

Это на это, это на это, это на это, это на это.

И складываю.

Я сотру, наверх напишу.

То есть, ПА у меня равен.

Давайте, что я сделаю?

32

двухсотых умножаю на 1 плюс 128 двухсотых умножая на одну вторую плюс 8 двухсотых умножая на одну вторую и 0 у меня получится 400 да ну можно в принципе сократить 64

Здесь 4.

Можно не 400, а 200 написать.

И посчитать.

У меня 32, 64 плюс 4.

Сколько будет?

68, 32.

Чему будет равно?

Одной, второй.

Вопрос ясен?

Да, понятно.

Ясно.

Теперь давайте формулу Бейса.

Здесь есть хорошая задача.

Давайте ее поработаем.

101 задача.

В специализированную больницу поступают в среднем 50% больных с заболеванием К. То есть больница... Сейчас я доску подготовлю, ребята, 2 минуты.

Значит, в больницу поступают три вида больных.

К, Л, М. В среднем 50% с заболеванием К, 30% с заболеванием Л и 20% с заболеванием М. Вот три вида больных.

Вероятность полного излечения, полного выздоровления заболевания К равно 0,7.

Это выздоровление.

Сейчас.

Это выздоровление.

Это поступление.

0,7.

Полное выздоровление для болезни М равно 0,8.

И полное выздоровление болезни М равно 0,9.

Значит, самый тяжелый больной К.

70%.

Теперь.

Больной, поступивший в больницу,

Был выписан здоровым.

То есть произвольно больной поступил.

Мы не знаем, какой болезни.

Поступил больной, он выписан был здоровым.

Теперь сделаем анализ.

Найти вероятность события того, что этот больной страдал заболеванием К. То есть самой тяжелой формы болезни.

То есть событие А. Основное событие.

Больной выздоровел.

Здоров.

Выздоровел.

Теперь давайте гипотезы распишем.

H1.

Больной болел болезнью К. H2.

Больной болел болезнью Л. H3.

Больной болел болезнью М. У меня три вида больных.

Больше других видов больницы не принимают.

Теперь давайте каждый раз пишем.

PH1.

Поступивший больной болеет болезнью К. Сколько процентов поступает?

50.

То есть 0,50 это будет 0,5.

PH2.

Больной болеет болезнью Л.

30%, 0,3.

И третье, больной болеет болезнью М, равно 0,2.

Потому что 20%.

Если больной болеет болезнью К, первой болезнью, то, что он выздоровеет, вот выздоровел, равно 0,7, ребята.

Если

Он болеет болезнью второй, то, что он выздоровеет, 0,8.

И PH3, третья болезнь, 0,9.

Что я говорю?

Я говорю, что больной выздоровел, то есть А событие произошло.

Вот я специально написала рядом.

То есть высчитывая А, 0,5 на 0,7.

Плюс 0,3 на 0,8.

Плюс 0,2 на 0,9.

Посчитайте, ребята, сколько это будет.

0,35, 0,24 и 0,18.

Сколько это будет, чтобы любой больной выздоровел?

Чему равно?

9,7.

Один в уме.

5,6,7.

0,77.

Правильно посчитала?

35, 9, 7, 1.

Да, да, 0,77.

5, 6, 7, 7.

Значит, больной, то, что любой больной выздоровеет, любой, какой бы болезнь он не болел, произвольный, это 0,77.

Но мне надо найти что, ребята?

Мне нужно найти, что больной выздоровел, вот, а выполнилось, если он болел первой болезнью, H1, вот это самое тяжелое слово.

Формула эта, смотрите, я давайте наверху напишу.

То есть PA выздоровел H1, у меня равен PH1 умножено PH1A, то есть вероятность гипотезы на условную вероятность, делю на PA. То есть, вот.

0,5 на 0,7 делю на 0,77.

Это 35,77.

То есть 35,77 будет равно 5,11.

Чему это равно?

5,11, что самый тяжелый больной выздоровел.

Точно так же вы можете посчитать,

Условные вероятности для каждого из этих больных.

То есть если вам в больнице говорят, делайте нам прогноз, анализ делается, числа же даются, количество, статистику дают.

Вот вам статистика, что выздоровеет больной второй.

Чему будет равно?

Знаменатель не меняется.

А наверху сколько у меня было?

0,3 на...

0,8.

То есть 24,77.

PAH3.

0,2 на 0,9.

0,77.

Это 18,77.

И сумма вот этих вероятностей должна быть равна у вас единице тоже, ребята.

PAHI, ребята,

И от 1 до n должно быть равно 1.

Если 1 не получится, значит вы здесь также.

Получается неправильное решение.

Вопрос ясен?

В чем заключается суть теоремы формулы Бейса?

Да, понятно.

Вот я вам давайте еще коротко доказательство, на слайде было сложно, откуда мы взяли формулу действия.

Я вам сказала, от умножения теоремы, ой, от вероятности произведения двух событий, а умножено на b, если они у вас зависимы.

Я говорила в прошлый раз, вероятность любого из них на условную вероятность второго,

что первое уже наступило.

Либо ПБ и ПА, что Б уже наступило.

Вот из этой формулы получается.

Вы должны найти вот эту часть.

То есть ПА у вас есть, Б должны найти.

Это будет ПА поделить.

Получаем мы что?

ПБ П

БА.

Деленная на ПА.

И если вы единственно сюда поставите что?

Гипотезы и поставите все.

Вот, пожалуйста.

Вот доказательства вашей формулы БЕГИСа.

Вопрос.

Вопрос есть?

Ребята,

Нет вопросов.

Давайте одну маленькую еще задачку.

Я вас отпущу буквально 5 минут.

99-я задача.

Число грузовых автомашин, проезжающих по шоссе, то есть по трассе, на котором стоит бензоколонка,

относится к числу легковых машин 3 к 2.

Вероятность того, что проезжающая грузовая машина заправится, равно 0,1.

А вероятность того, что заправится легковая машина, равно 0,2.

С беззаколонки подъехала машина для заправки.

Найти вероятность того, что эта машина грузовая.

Значит, что мы должны найти?

Во-первых, событие А у нас.

Машина заправилась.

Мы не знаем, какая.

Просто заправилась.

Беззаколонка заработала деньги.

Заправилась.

Какая машина заправилась?

H1.

Грузовая машина подъехала.

H2.

Легковая машина подъехала.

Ребята, отношение подъезжания грузовой к легковой равно 3 к 2.

То есть

Появление H1 у вас равно, так как 3 к 2, 3 к 5 будет.

То есть грузовая, раз отношение H1 на H2 у вас 3 к 2, сумма 5, отношение 3 к 5.

То, что подъедет легковая, будет равно 2 к 5.

Ну, как Кабулов сказал, 60%, здесь 40% в процентном соотношении.

Теперь, это подъехало.

То, что проезжает грузовая и она заправится, равно 0,1.

То, что подъедет легковая и она заправится, равно 0,2.

Мне надо найти, что машина заправилась.

Но заправилась какая?

Грузовая, первая.

Оно равно PH1, PH1A и деленное на PA. Можно сразу написать PH1, вот у вас, 0,6 на 0,1, а PA, соответственно, это на это, 0,6 на 0,1,

Плюс 0,4 на 0,2.

Равно.

Давайте я вот сюда напишу.

0,06 деленное здесь сколько будет?

0,06 плюс 0,08.

То есть 6,14.

В итоге получится 3,7.

То, что у меня заправится грузовая машина.

Вопрос ясен?

Да.

Задача ясна?

Если вы, соответственно, хотите найти того, что заправится машина и заправится легковая, естественно, будет здесь у меня 14, получилось 0,14, а наверху будет 0,4 на 0,2.

То есть 8,14 это будет 4,7.

Вот мы правильно вам посчитали с вами.

3 седьмых плюс 4 седьмых, вы, соответственно, посчитали, чему равно то, что легковая заправится, чему равно то, что грузовая заправится.

Сумма этих вероятностей, я так вам сказала, всегда составляет полную группу, и оно равно единице должно быть.

Вопрос ясен, ребята?

Да.

На этом я с вами, в принципе, формулу длинницы закончила.

Есть вопросы, если есть, задавайте.

Если нет, то на сегодня я закончу.

Так.

Старайтесь в модуле, значит, каждый... Я RGR вам отправила своим ребятам.

Вы, наверное, получили.

Первый RGR и для бухгалтеров, и для экономистов, менеджмент, маркетинг, задание...

Ну, задачи разные, просто одинаковые.

А второе будет отличаться.

Мы через две лекции, наверное, я вас разделю уже.

Я буду объявлять, когда для бухгалтеров, когда для экономистов, для менеджментов.

Там уже вероятность свою часть закончу, потом будет разница у нас.

Другая лекция будет отличаться.

Если вопросов нет, то до свидания.

До свидания.

Спасибо.

До свидания.

Всего доброго, ребята.

Отдыхайте.