Эшмаматова Экономическая математика лекция 7
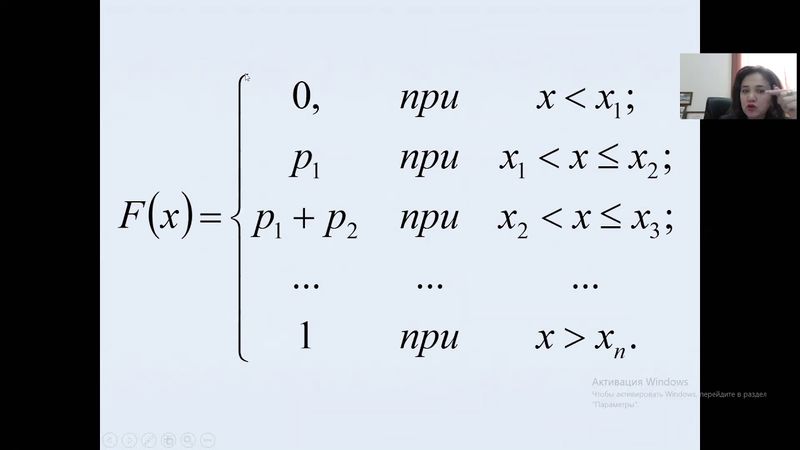
Информация о загрузке и деталях видео Эшмаматова Экономическая математика лекция 7
Автор:
Dilfuza EshmamatovaДата публикации:
29.10.2020Просмотров:
13Транскрибация видео
Так, случайные величины.
Здравствуйте.
Здравствуйте еще раз.
Значит, у нас сегодня с вами тема случайной величины.
Так.
Дискретная случайная величина.
Значит, во-первых, давайте так.
Сегодняшний план лекции у нас с вами.
Виды случайных величин.
Так, распределение дискретно-случайной величины, функция распределения, числовые характеристики дискретных случайных величин.
Значит, вопросы мы в конце посмотрим с вами.
Какие случайные величины бывают?
Значит, виды случайных величин.
Первое.
Первое, значит, дискретная случайная величина.
Что это такое?
Значит, смотрите.
Вообще величина называется случайной, вообще, ребята, если в результате опыта она может принимать любые заранее неизвестные значения.
То есть поэтому и называется она случайной.
То есть...
В общем виде, смотрите.
Величина называется случайной, если в результате опыта она может принимать любые, любые заранее нам неизвестные значения.
Поэтому и называется она случайной.
Какие виды?
Значит, первая случайная величины бывает двух видов.
Первая дискретная случайная величина и непрерывная случайная величина.
Теперь...
Дискретная случайная величина, как сокращенно будем с вами писать DSV.
Это случайная величина, которая принимает отдельное, то есть изолированное, и счетное множество значений.
То есть случайная величина, если будет принимать значение, которое, просто говоря, посчитать можно, счетное, то оно называется дискретной случайной величиной.
Теперь.
Теперь, сейчас, секундочку, ребята.
Непрерывная случайная величина.
Это случайная величина, которая принимает любые значения из какого-то промежутка.
Почему промежуток?
Потому что промежуток может быть бесконечным, ребята.
Любой промежуток, если взять интервал, внутри интервала всегда любые значения, которые очень...
плотно распределены, то есть между любыми двумя значениями всегда можно найти еще третье значение.
Например, давайте примеры посмотрим.
Значит, число посетителей, например, в поликлинику, вот сколько больных придет, в принципе, их можно посчитать, то есть они принимают счетное значение, поэтому оно и будет дискретно случайной величиной.
А непрерывная случайная величина, то же самое, например, вы больной, ну не вы, а вообще больной какой-то, значит,
Либо масса в каком-то промежутке какого-то времени будет принимать таблетки.
Этот промежуток времени может быть бесконечным.
Поэтому оно и будет, эта случайная величина и будет непрерывной случайной величиной.
Теперь, запомните, случайная величина обычно обозначаем большими буквами, а их значения маленькими.
Соответственно, если у вас х случайная величина, то ее значение можем х1, х2, х3 и так далее, хn обозначать.
Теперь, что такое распределение случайной величины?
Закон распределения случайной величины, то есть это...
Соответствие между возможными принимаемыми значениями случайной величины с его соответствующими вероятностями.
Этот закон называется законом распределения.
То есть вы... Смотрите.
В табличном виде, если взять вот x случайная величина, принимает значение x1 с вероятностью p1, x2 с вероятностью p2 и так далее, xn с вероятностью pn.
То есть x это все значения случайной величины, которые она принимает, а p1, p2 и так далее это ее вероятности,
с которыми эти значения принимает наша случайная величина.
В данном виде у нас дискретная случайная величина.
Вот эта таблица называется закон распределения дискретной случайной величины.
Теперь, если в одном испытании случайная величина принимает только одно возможное значение,
получаем, что событие x1 равен x, x равен x1, x равен x2 и так далее.
Тогда вот это все образует полную группу.
Следовательно, так как они принимают, вот смотрите, x1, x принимает
значение x1 с вероятностью p1, принимать x2 с вероятностью p2 и так далее, xn с вероятностью pn.
То есть полностью, если все это взять, они образуют полную группу, поэтому их вероятности по таблице всегда должно быть равно единице.
То есть в законе распределения дискретно случайной величины сумма вероятности должно всегда равняться единице.
Теперь, если мы возьмем вот эту таблицу, ребята, вот, и значение х разложим на оси ОХ, значение П распределим по у, то есть по оси абсцисс от П, тогда...
Значит, в таком случае x сюда, p1 туда, мы получим, соответственно, вот эти пары точек мы определим, смотрите, x1, p1, x2, p2 и так далее, xn, pn и так далее.
И мы эти точки, всех их если объединим,
мы получим многоугольник распределения.
Это вот этот рисунок, то есть любой, значит, например, вот закон распределения любой дискретно случайной величины можно графиками изобразить.
То есть вы берете точки, пары координатами x и pi и, значит, вот так расставляете на координатной оси.
И объединяя их, получаем
Значит, многоугольник распределения.
Теперь.
Если вас потребует построить многоугольник распределения, вы берете координатную плоскость и обозначаете пару этих точек и объединяете.
Это называется многоугольником распределения.
Теперь функция распределения.
Что такое функция распределения?
Внимательно слушаем.
Функция распределения случайной величины, я не говорю дискретной, любой случайной величины х, называется функция действительно переменной х, которая определяется равенством вероятность случайной величины х, посмотрите, тех значений случайной величины, которые принимает значение меньше, чем х. То есть,
Функция распределения называется вероятность случайной величины, принимаемой меньше значения х. То есть вот эта функция, которая определяется px меньше х, называется функцией распределения.
Иногда мы ее называем интегральной функцией распределения.
Значит, теперь...
Например, вот смотрите, как мы ее определяем внимательно, как мы получаем fx, px меньше x. Ну, смотрите, я вам еще раз повторяю, функция распределения, ребята, определяется одинаково и для дискретной случайной величины, и для непрерывной случайной величины.
Вот, смотрите, в некоторой литературе говорится функция распределения, в некоторой литературе интегральная функция.
То есть это идентичные определения, названия.
Теперь давайте посмотрим.
Если до значения, так как, смотрите, первое значение у нас х1.
Если до значения х1 случайная величина х не встречалась, то есть нету х меньше х1, первое значение х1, то и вероятность этого события х меньше х1 всегда равна нулю, ребята, всегда.
Теперь, для всех значений и от х1 до х2
вероятность события x меньше x, совпадает с вероятностью значения x1.
Вы берете p1.
Вот я как составить эту функцию объясняю.
Но когда х больше х2, случайная величина может принимать две возможные значения, то есть х1 и х2.
Поэтому, ребята, когда у вас х2, х больше х2, то есть х принимает значение от х2 до х3, вероятность будет равна p1 плюс p2 и так далее.
Если больше х3, естественно, p1 плюс p2 плюс p3 будет.
То есть в табличной форме, как функцию если взять, мы получаем для функции распределения вот такую таблицу.
Теперь, то есть функция распределения, то есть интегральная функция, имеет вот следующий вид.
Смотрите, 0 равен, когда х меньше х1, p1, х от х1 до х2,
p1 плюс p2, x от x2 до x3 и так далее, единица при x больше xn.
Вот это общая форма нахождения функции распределения я. Теперь.
Если мы графически изобразим вот эту функцию, если взять график этой функции, мы получим с вами ступенчатую функцию.
То есть она будет монотонная.
Как вы видите, у вас вероятность, фактически ее значение возрастает, но максимальное значение этой функции, вот смотрите, единица.
То есть функция, даже по схеме видно, что функция имеет значение от нуля до единицы.
Давайте теперь эту функцию изобразим на плоскости, то есть на оси О и Х поставим ординат, поставим функцию F от Х.
Ну и получим вот следующее.
Значит, смотрите, вот до x1 0, видите, вот черными мы, вы обязаны его вот так обозначить.
От x1 до x2, значит, p1.
От x2 до x3, значит, p1 плюс p2 и так далее.
От xn до бесконечности p1 плюс p2 и тогда pn.
То есть это у вас равно единице, ребята, вот это.
Здесь вместо него равно единицу надо поставить, я забыла.
Теперь, это значит, как вы видите, график интегральной функции является ступенчатой функцией, которая принимает значение от нуля до максимум единицы.
Вот если вы свойства сейчас, в принципе, по графику уже можем мы свойства этой функции определить.
То есть, смотрите, первое,
У нас функция, ребята, принимает значение от 0 до 1.
Это первое свойство.
То есть вот.
Оно не может быть меньше 0 и не может быть больше 1.
Почему?
Само определение этой функции говорит об этом.
Почему?
Ну-ка, вспомним определение, ребята.
Почему от 0 до 1 функция?
Потому что эта функция определяется вероятностью.
То есть функция фактически это вероятность, видите?
А вероятность может принимать значение от 0 до 1.
Поэтому значение этой функции тоже будет всегда от 0 до 1.
Теперь запомните, функция является монотонной, то есть она не убывающая.
То есть для любых x1 меньше x2 выполняется вот это неравенство.
То есть, соответственно, значение функции тоже будет
Не больше для этих значений, соответствующих значениям.
Теперь, числовые характеристики дискретных случайных величин.
Давайте я сначала думала все случайные величины дам, потом числовые характеристики.
Нет, давайте лучше отдельно дам, чтобы вам было легче.
У вас на ВРГР тоже отдельно идут там задачи, поэтому.
Значит, числовые характеристики дискретных случайных величин.
Первое.
Математическое ожидание и его свойства.
Что такое математическое ожидание?
Значит, смотрите.
Математическое ожидание дискретной случайной величины
Называется сумма произведения значений случайной величины соответствующими их вероятностями.
То есть...
Еще раз повторяю, смотрите теперь по определению.
С математическим ожиданием дискретной случайной величины х называется сумма произведений всех ее значений на соответствующие вероятности.
То есть это х1 на p1 плюс х2 на p2 и так далее, плюс хn на pn и так далее.
Вот сумма х и п и.
Теперь, что означает, что это такое математическое ожидание вообще?
Свой смысл, вероятностный смысл в чем заключается?
Математическое ожидание фактически это среднее значение наблюдаемых...
значений вот этой случайной величины.
Это фактически среднее значение.
Это более... Вот смотрите, любой, как я вам только что сказала, дискретно случайная величина вообще определяется своим законом распределения, многоугольником, функцией распределения.
Но
А математическое ожидание – это уже его характеристика.
Характеристика, она более точное значение дает, и оно, смысл его заключается приближенно, оно в чем?
Оно равно среднему арифметическому наблюдаемых значений случайной величины.
То есть на часовой оси, если посмотреть, возможное значение вот этой случайной величины,
расположена слева и справа от математического ожидания.
То есть математическое ожидание больше наименьшего и меньше наибольшего значения.
То есть оно дает среднее значение всех наблюдаемых значений данной случайной величины.
Теперь, какие свойства математического ожидания?
Самое первое свойство –
Математическое ожидание константы, то есть постоянной, равно самой постоянной, ребята.
То есть mc равен c. То есть если, смотрите, если у вас случайная величина, дискретно случайная величина, насчет дискретной случайной величины, сейчас разговор идет, принимает только одно значение, то есть, например, оно принимает значение 5.
Естественно, если оно других значений не принимает, то это значение принимает с вероятностью 1.
Поэтому математическое ожидание будет равно С, ребята.
Теперь самой себе.
То есть МС равен С умноженное на 1.
Это будет С. Запомните, постоянный множитель можно выносить за знак математического ожидания.
То есть mcx это c умножено mx.
Это второе.
Теперь математическое ожидание суммы конечного числа случайных величин, ребята.
То есть если у вас идет сумма 2 и более конечного числа случайных величин, то математическое ожидание от суммы равно сумме математических ожиданий этой случайной величины.
То есть mx плюс my.
Теперь, смотрите, математическое ожидание произведения двух или более только конечного числа случайных величин равно произведению их математических ожиданий, ребята.
То есть...
только при условии, что эти математические ожидания, ой, дискретно случайные величины должны быть независимые.
Значит, математическое ожидание конечного числа независимых случайных величин равно их произведению математических ожиданий.
То есть mx умножено на y равен mx умножено на my.
Теперь дисперсия.
Это вторая, значит, числовая характеристика случайной величины, дискретно случайной величины.
Дисперсией, рассеянием, то есть, как его, ну, слово дисперсия, его расшифровка, то есть перевод, это означает рассеяние.
дискретно случайной величины, называется математическое ожидание квадрата отклонения случайной величины квадрата отклонения случайной величины от ее математического ожидания.
Вот смотрите, что я сказала.
Дисперсия это математическое ожидание m квадрата
отклонение x минус mx, отклонение этой случайной величины.
То есть, еще раз повторяю, дисперсия дискретной случайной величины, по определению я иду, смотрите, математическое ожидание, отклонение, то есть разности, этой случайной величины,
То есть квадрат отклонения, квадрат я забыла, квадрат отклонения, то есть разности дискретно случайной величины от его математического ожидания.
Свойства какие?
Значит, только что я вам сказала...
Значит, математическое ожидание от постоянной было равно самому себе числу.
А дисперсии нет.
Дисперсия с постоянной величиной равна, оказывается, нулю, ребята.
Вы можете это доказать.
Вот здесь вместо х поставить s. Раскрыть и увидеть.
Я вам чуть попозже объясню.
Сейчас я вам дам их доказательства.
Теперь.
Постоянный множитель можно выносить за знак дисперсии, возводя его только в квадрат.
То есть dsx это равно будет s2 умножено dx.
Теперь дисперсия суммы конечного числа случайных величин равна сумме их дисперсии.
Вот, пожалуйста, dx плюс y равен dx плюс y.
Теперь, вот смотрите, вот это, ребята, по определению вообще, само определение, вот я вам сказала, что математическое ожидание, квадрат, отклонение, случайные величины от его математического ожидания.
Но эта формула очень неудобна для работы.
То есть, когда вы работаете для вычисления дисперсии, она неудобна.
Поэтому я приведу вам теорему.
Она дает нам формулу для вычисления дисперсии.
То есть дисперсия дискретной случайной величины равна разности между математическим ожиданием квадрата случайной величины
и квадратом ее математического ожидания.
То есть dx равен mx квадрат, то есть математическое ожидание x квадрата минус mx в квадрате.
Теперь, эту формулу я вам, смотрите, завтра, сейчас я до конца добью, потом вам доказательства приведу.
Теперь смотрите, среднее квадратическое отклонение.
Это третья характеристика у нас с вами.
Значит, среднее квадратическое отклонение случайной величины называется арифметическое значение квадратного корня из ее дисперсии.
Как вы видите, так как среднее квадратическое отклонение является квадратным корнем, значит дисперсия не может быть отрицательным.
Если вы когда решаете, у вас дисперсия получается отрицательным числом,
Значит, вы неправильно этот пример решили.
Понятно, да?
То есть дисперсия не может принимать отрицательные значения.
Например, смотрите.
Вычислить математическое ожидание, дисперсию, среднее квадратическое отклонение, дискретный случайный величинный х, определяемый как количество студентов в наугад выбранной группе, используя следующий пример.
Следующие данные.
8 студентов 0,2 вероятностью, 9 – 0,1, 10 – 0,3, 11 – 0,2 и 12 – 0,2.
Сумма сколько будет?
6.
Вот сумма единицы.
Значит, вот
Дискретная случайная величина, х у нас, определяется количество студентов наугад выбранной группы.
Сколько может быть студентов, например, вот я зашла в группу, хочу проверить, сколько сидят студентов.
8 студентов, вероятность 0,2, 9 студентов, вероятность 0,1, 10, 0,3, 11, 0,2 и 12, 0,2.
Мы должны найти математическое ожидание дисперсии и среднее квадратическое отклонение.
Формула у нас есть с вами.
Давайте поехали.
Мх.
Чему равно Мх?
8 на 0,2 плюс 9 на 0,1, 10 на 0,3, 11 на 0,2, 12 на 0,2.
Например, вот, пожалуйста.
То есть математическое ожидание равно 10,1.
Теперь, поняли, да, или нет?
Теперь давайте попробуем найти дисперсию.
Что такое дисперсия была?
Для дисперсии мы берем по теореме ту формулу mx квадрат минус mx в квадрате.
То есть dx это вы берете 8 в квадрате умножаете на 0,2.
9...
квадрате на 0,1 плюс 10 в квадрате на 0,3 плюс 11 в квадрате на 0,2 и 12 в квадрате на 0,2.
То есть в итоге мы получаем, вот смотрите, квадраты возвели, но вероятность не трогаете.
Значение возводите в квадрат, вероятность остается так же.
И минус mx в квадрате.
Вот, пожалуйста, dx нашли мы с вами.
А σx у нас корень из этого dx.
Вот мы полностью эту задачку с вами
Решили.
То есть мы с вами нашли и математическое ожидание, и дисперсию, и среднее квадратическое отклонение.
Вопросы есть?
Нет.
Теперь, смотрите, если проводится вот несколько испытаний, одно и то же,
И надо найти математическое ожидание и дисперсии числа появлений этих событий в независимых испытаниях.
То есть одно и то же событие в этих испытаниях принимает одно и то же вероятность.
Например, вы сто раз бросаете монету.
Например, найдите математическое ожидание и дисперсию числа появления, например, скажем, герба в этих сто раз.
Надо математическое ожидание найти и дисперсии.
Запомните, если вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то есть каждое испытание независимо друг от друга, то какие такие испытания, естественно, назывались у нас с вами независимыми.
Это определение у нас было.
И пусть эти вероятности одинаковые.
То есть в каждом из этих бросаний, например, монеты, у вас каждый раз одна и та же вероятность.
То есть то, что герб попадет, у нас одна вторая.
Тогда вероятность...
Не наступление, у вас помните, Q было.
Если P мы берем за вероятность наступления события A, Q это будет не наступление события A. Тогда, ну, Q это 1 минус P. Теперь математическое ожидание, ребят.
Теорема, смотрите.
Математическое ожидание числа появлений события A
В независимых испытаниях равно произведению числа испытаний на вероятность появления события А в каждом испытании.
То есть МХ равен Н умножено П. То есть если мы 100 раз бросаем монету грубо, и надо найти математическое ожидание числа появлений Герба, например.
Н у вас равен 100.
П – одна вторая.
Математическое ожидание будет равно 50.
Теперь, то есть в таких случаях таблицу рисовать не обязательно.
Теперь дисперсия.
Дисперсия числа появлений события А в независимых испытаниях равна произведению числа испытаний на вероятности появления и непоявления.
То есть дисперсия равна НПК.
Есть у некоторых ребят эти задачи.
По-моему, шестая задачка была такая на эти формулы.
Теперь, например, в пяти аптеках проверяется годовой баланс.
Вероятность правильного оформления баланса в каждой аптеке равна 0,7.
То есть разница в какой аптеке?
В одной, во второй, в третьей, тогда и в пятой 0,7.
Найти математическое ожидание и дисперсию правильно оформленных балансов.
n у вас 5, вероятность у вас 0,7.
А неправильное оформление это 0,3 у вас будет.
Вот теперь математическое ожидание находим.
Математическое ожидание будет равно у вас n на p, то есть 5 на 0,7, 3,5.
А дисперсия равно 5, 0,7 на 0,3, 1, 0, 0,5.
Ну, среднее квадратическое отклонение, естественно, вы берете dx и с корня извлекаете.
Вопрос ясен, ребята?
Да.
Вот мы с вами полностью разобрали дискретную случайную величину.
Значит, смотрите.
Что по случайной величине вы должны знать?
Я сейчас пока не остановилась с непрерывной случайной величиной.
Только дискретная случайная величина.
Что такое вообще случайная величина?
Вот вопросы.
Первое.
Эти же вопросы будут на ПК, ИК, то есть они будут в виде тестов только.
Какие виды случайных величин знаете?
То есть виды я вам сказала, два вида.
Дискретная случайная величина и непрерывная случайная величина.
Какие величины называются дискретной, а какие величины называются непрерывной?
Определение я вам его дала сегодня.
Что такое закон распределения любой случайной величины?
Как можно задать закон распределения случайной величины?
Как можно задать закон распределения дискретной случайной величины?
И основные числовые характеристики дискретных случайных величины и формулы их вычисления.
Значит,
Закон распределения дискретно-случайно величины я вам показала, но в табличном виде.
Его еще графически можно представить.
Потом функцию распределения я вам показала, какой вид у нее.
Ее тоже график, она ступенчатая, ее свойства мы с вами посмотрели.
И числовые характеристики, то есть математическое ожидание, дисперсия и среднее квадратическое отклонение.
Вот, и все формулы по их, как их вычислять.
Вопросы по дискретным случайным величинам есть, ребята?
По примерам.
Нет, нет, нет, пока нет.
Смотрите, у меня, вот сейчас, если нет, значит...
Так, на сегодня все.
Если у вас вопросов нету, я закончила.
Спасибо.
Так, ребята, у вас РГР вы получили, правильно?
Да.