Видеолекци 5 ТВ и МСТ БНТУ

Так, здравствуйте, уважаемые студенты.

Здравствуйте, здравствуйте.

Здравствуйте, рада вас слышать.

Видеть пока не могу.

Можно такой вопрос.

Вы на какое обучение согласились, на онлайн или оффлайн?

Онлайн.

У вас пока онлайн, да, или как?

Онлайн, онлайн.

Хорошо.

Если онлайн, давайте так, мы, вот мы, я никакое расписание не меняю.

Четверг, суббота мы с вами проводим занятия.

Хорошо, ребята?

Все.

Хорошо, хорошо.

Ориентир где-то 11 часов.

Ну, исходя из того, что какие у вас занятия, мы можем его с вами оговаривать время, если что.

Договорились, да?

Чтобы вам тоже удобно было и мне.

Договорились, ребята?

Но занятия должны проводиться четверг и суббота обязательно.

Так.

И сейчас демонстрацию экрана включу.

Так.

Так, слайд виден, ребята?

Да.

Так, значит, сегодня у нас с вами следующая лекция.

Тема нашей лекции – случайные величины.

Тема конкретной – дискретные случайные величины.

Так, значит, что такое…

вообще случайная величина.

Давайте сначала мы сегодня с вами обсудим сначала план нашей деятельности.

Какие виды случайных величин существуют, то есть виды случайных величин, распределение дискретной случайной величины, функции распределения, числовые характеристики дискретных случайных величин.

Значит, до числовых характеристик, ну, посмотрим, я дойду или нет, но до первые три пункта мы с вами сегодня обязаны

обсудить, почему я говорю четвертую попозже, может быть, я посмотрю, потому что числовые характеристики для определения числовых характеристик я могу дать вам после непрерывных случайных величий, поэтому я

По ходу действия будем смотреть, скажем так.

Какие вопросы должны быть?

Смотрите, что такое случайная величина?

Какие виды случайных величин вы знаете?

Эти вопросы будут у вас в итоговом контроле, поэтому я включила их в презентацию.

Что такое вообще дискретная случайная величина, то есть определение дискретной случайной величины?

Что вы понимаете под законом распределения случайной величины?

И как можно задать распределение случайной величины в закон распределения?

И как можно задать закон распределения именно дискретной случайной величины?

Назовите основные характеристики и для дискретно случайных величин и запишите их в отчисления.

Теперь.

Давайте, первый пункт.

Виды случайных величин.

Какого вида существуют случайные величины?

Значит, вот смотрите.

Вообще, что такое случайная величина, ребята?

Случайная величина...

Это та величина, которая может принимать в результате опыта заранее неизвестные любые, значит, случайные нам значения.

То есть величина называется случайной.

Само определение говорит за себя, ребята.

Если в результате опыта она может принимать любые заранее неизвестные значения.

То есть случайно она может принимать любые значения, которые нам неизвестны.

Значит, это понятие вообще случайная величина очень...

является одним из важных понятий в теории вероятностей.

Дальше мы будем даже рассматривать в математической статистике тоже, но чуть-чуть формулировку будем менять и понятие поменяется, увидим мы дальше с вами.

Это будет в последующих наших лекциях.

Значит, какого вида бывает случайная величина?

Оказывается, двух видов.

Первая – дискретная случайная величина.

Мы с вами будем обозначать ДСВ.

Вторая – непрерывная случайная величина – НСВ.

Дискретная случайная величина – это случайная величина, ребята, которая принимает счетное или конечное значение.

То есть дискретная, вот если грамотно мы с вами это понимаем,

Обсудим, значит, определение дадим.

Дискретно случайная величина – это та величина, которая принимает отдельно изолированные и счетные, как я вам сказала, счетные множество значений.

То есть, такая величина, значение которой можно посчитать.

Теперь, и конечная.

Например, число поликлиники, число посетителей, то есть больных, поликлиники в течение дня.

Посчитать можно, бесконечно не может быть.

Либо непрерывная случайная величина.

Это величина, смотрите, которая, значит, то есть принимает бесконечную, само по себе называется бесконечная, непрерывная случайная величина.

Это случайная величина, принимающая любые значения из некоторого промежутка.

Как мы с вами знаем, промежуток это, например, если числовую ось взять, 0,1 промежуток.

Если взять, например, хоть оно и ограничено, ребята, но там...

в отрезке 0,1 числа очень...

как говорится, плотно расположена, то есть там бесконечно много чисел.

То есть в этом отрезке между любыми двумя цифрами можно всегда найти третье число.

Поэтому если случайная величина, например, принимает значение из-за отрезка, например, 0,1 или от А до Б, то есть какой-то промежуток в такой, такие случайные величины называются непрерывными случайными величинами, ребята.

Теперь

Например, вот таблетка.

Наугад выбираю таблетку.

Масса любой выбранной таблетки препарата.

Во-первых, оно может быть бесконечно.

То есть разные таблетки, ребята, мы ограничить с вами не можем.

То есть ограниченным не можем.

Поэтому вот этот пример тоже будет примером непрерывной случайной величины.

Теперь.

Случайные величины всегда обозначаются большими буквами.

А, ой, х, у, з, там и так далее.

А их значение соответствует, вот какая случайная величина, маленькая, маленькая буковка будет ее значение.

Х, х, у, у, з, з и так далее, ребята, строчные буквы.

Теперь, например, если случайная величина х, вот смотрите, имеет 3 принимает значения, значит мы обозначаем, соответственно, х1, х2, х3.

Если у, то у1, у2, у3 и так далее.

Если 5 значений, естественно, х4, х5 у вас добавится.

Теперь, вот так вот пишется, вот в таком виде, ребята.

Закон распределения случайной величины, дискретной случайной величины.

Что такое, я сначала вам объясню.

Закон распределения дискретной случайной величины – это соответствие принимаемой случайной величиной

и ее соответствующими вероятностями.

То есть, другими словами, законом распределения называют соответствие возможными значениями и их вероятностями.

Вот грамотно это.

Теперь, то есть x принимает, например, значение x1, x2, x3 с вероятностями, соответствующими p1, p2, p3.

Вот я вот устно сказала, это таблица.

Вот в виде таблицы мы можем.

Можно графические представить, можно в виде таблицы, можно в виде формулы.

Обычно в виде формулы обозначается закон распределения непрерывной случайной величины.

Для дискретных случайных величин обычно в виде таблицы и графические.

Ну формула тоже, но...

Редко.

При табличном задании вот, пожалуйста, можем видеть.

Вот смотрите, первая строка – это значение случайной величины, которую она принимает, х1, х2 и так далее, хn.

А нижняя – это соответствующие ее вероятности, p1, p2 и так далее, pn.

Вот, пожалуйста.

Теперь, значит, смотрите.

Если случайная величина в одном испытании принимает одно и только одно возможное значение, вот x1, x2 и так далее, и так как эти все значения образуют полную группу, запомните, сумма их вероятностей всегда равна единице.

P1 плюс P2 и тогда плюс Pn равен 1.

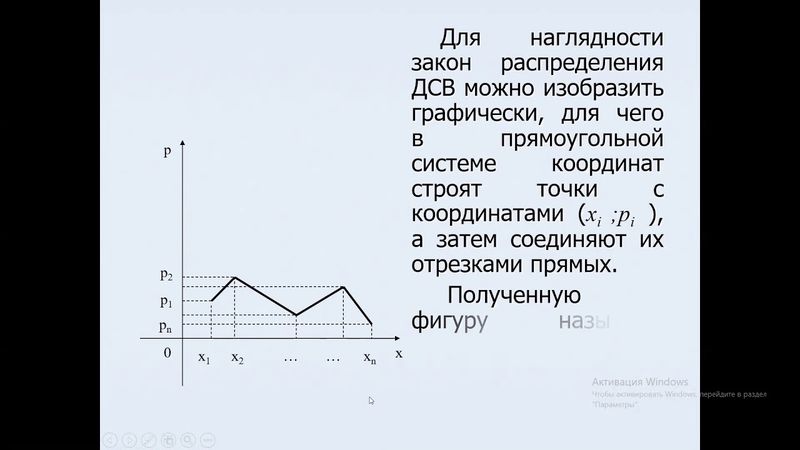
Если мы вот эту таблицу изобразим на плоскости, то есть в декартовой системе координат, мы получим следующий вид.

Смотрите, вот, пожалуйста.

То есть x мы будем изображать на числовой оси абсцисс, а p вероятность на ординате.

То есть от 0 до p будет у нас.

Естественно, так как вероятность максимального значения 1, вот, пожалуйста, здесь x1, p1, x2, p2 и так далее, xn, pn.

Вот я вам только что сказала, прямоугольной системе координат.

То есть мы, эта фигура называется многоугольник распределения.

То есть мы с вами на координатной оси, декартной системе координат, обозначаем точки х и п, и, как я вам сказала, вместо у ставим п, и эти точки потом объединяем, получаем с вами, значит...

как его, многоугольник.

Функция распределения.

Функция распределения случайной величины х называется функция действительной переменной х1 или просто х. Вот смотрите, запомните.

Функция распределения — это функция, зависящая от х. Это вероятность...

Событие, когда х меньше х, принимает значение меньше х. То есть, смотрите, функция распределения – это вероятность события, когда случайная величина принимает меньше значения, чем х, ребята.

Эта функция называется функцией распределения.

Другими словами, ее можно назвать интегральной функцией.

Это определение работает и для дискретной случайной величины, и для непрерывной случайной величины.

То есть какого типа она ни была, для нее функция распределения или интегральная функция, определение интегральной функции, это вероятность того, что случайная величина принимает

значение меньше, чем x. Определение понятно, ребята?

Теперь, какие свойства существуют?

Я здесь не привела, я вам устно объясню.

Во-первых, оказывается, эта функция является

Положительный, то есть больше либо равно нуля.

Отрицательным она быть не может.

И эта функция принимает значение от нуля до единицы.

Почему, как вы думаете?

Ребята, почему?

Почему?

Как вы думаете?

Потому что само определение говорит за нее.

Смотрите, функция определяется как вероятность, а вероятность не может быть больше единицы и меньше нуля.

То есть так как само определение функции это вероятность какого-то события, то есть события того, что х принимает меньше, чем х значение, поэтому значение этой функции...

функция принимает значение от 0 до 1.

Это первое.

Во-вторых, функция является монотонной.

То есть, если мы возьмем два значения x1 и x2, и у вас x1 меньше x2, естественно, соответствующие значения

этой функции fx1 тоже будет меньше чем значение x2 то есть чем растет значение аргумента тем растет значение и функции поэтому эта функция является монотонной теперь давайте посмотрим как мы можем найти вычислить эту функцию вот смотрите

До первого значения, до x1, случайная величина не встречается, поэтому вероятность того, что событие принимает значение x, принимает значение меньше x1, всегда 0.

Для всех значений от x1 до x2 вероятность события x меньше x совпадает с вероятностью значения x1.

То есть это будет p1.

Но при значении x больше x2 случайная величина может принимать два значения x1 и x2.

Поэтому и складываются их вероятности p1 плюс p2.

И так далее.

Мы получаем вот следующую схему.

Если дискретное...

значения случайной величины от x1 до xn, то есть x1, x2 и так далее, xn, расположены в порядке возрастания, обязательно вы должны порядок возрастания учесть, то каждому значению x и этих величин ставится соответствие суммы вероятности всех предыдущих значений p и. То есть x1 это p1, x2 p1 плюс p2, x3 и так далее.

Вот, пожалуйста.

Теперь, поняли, ребята?

Молчите, значит, поняли.

Теперь приведем вид нашей функции.

Значит, 0 при x меньше x1.

От x1 до x2 это p1.

От x2 до x3 это p1 плюс p2.

И так далее.

Единица равен при х больше х1.

Вот общий вид вычисления, то есть нахождения функции распределения данной случайной величины.

Для любой.

Опять-таки я говорю для любой.

Если мы с вами...

Значит, графически хотим изобразить эту функцию.

Естественно, значение х мы раскладываем на оси х, а значение вероятности на оси у. До х1, вот мы черными сделали, это 0.

От x1 до x2 это p1, вот p1.

От x2 до x3 p1 плюс p2, как вы видите, и так далее.

От xn и больше у меня вот эта сумма p1 плюс p2 плюс и так далее pn, это единица, ребята.

То есть максимальное значение функции это вот эта единица, вот 1 здесь будет, надо написать равно 1, ребята.

Здесь не написала, я извиняюсь.

А здесь 0.

Вот график нашей функции распределения или интегральной функции для нашей случайной величины.

Как вы видите, она ступенчатая функция.

Вопросы есть по графику?

Вот график, еще раз говорю, функции распределения случайной величины.

Теперь,

Вот то, что я вам устно сказала.

Вот теперь записываем с вами свойства.

Первое свойство, как я вам сказала, значение функции от 0 до 1.

Второе.

Для двух значений x1 меньше x2 соответствует значение функции fx1 меньше равно fx2.

То есть функция является монотонной.

Теперь, ну давайте хорошо числовые характеристики, я вам сегодня, у меня пока время есть, для дискретной покажу, потом в следующий раз для непрерывной случайной величины.

Какие, значит, числовые характеристики могут быть?

Первая, самая главная числовая характеристика – это математическое ожидание.

Так, ребята, естественно, любая случайная величина, она определяется, то есть излагается своим законом распределения.

то есть интегральной функции, но оно является характеристикой, но еще точнее характеристику дает математическое ожидание случайной величины.

Теперь математическим ожиданием дискретной случайной величины х

Называется, ребята, сумма произведений всех ее значений на соответствующие вероятности.

Все, ничего сложного.

То есть вы x1 умножаете на p1, плюс x2 на p2, плюс x3 на p3 и так далее, xn на pn.

Это называется математическим ожиданием.

Вот, пожалуйста.

То есть в таблице берете значения, умножаете соответствующие значения и их складываете.

Вот, пожалуйста.

Какой вероятностный смысл имеет математическое ожидание?

Математическое ожидание, оказывается, ребята, приближен... Давайте...

вероятностный смысл объясню, оказывается математическое ожидание приближенно равно среднему значению, то есть среднему арифметическому значению наблюдаемых значений случайной величины.

То есть вы, когда рассматриваете закон распределения или интегральную функцию, вы отдельно значения смотрите.

А вот математическое ожидание равно среднему арифметическому всех значениям.

То есть берется среднее значение.

То есть на числовой оси возможные значения расположены слева направо от математического ожидания.

То есть, что это значит?

Математическое ожидание – это такое характеристика числа, которое больше наименьшего и меньше наибольшего возможных значений.

То есть оно дает общую среднюю картину для нашей случайной величины.

Свойства математического ожидания.

Математическое ожидание постоянной величины равно самой постоянной, ребята.

Запомните.

То есть если у вас случайная величина принимает одно значение, математическое ожидание его равно самому этому значению, ребята.

Теперь второе.

Так, теперь, значит, постоянный множитель, оказывается, можно выносить за знак математического ожидания, то есть вот mcx, вы можете c просто, чтобы не мешало, вынести за знак и посчитать само математическое ожидание данной случайной величины.

Следующее, третье, математическое ожидание суммы двух либо n конечного числа случайных величин равно сумме их математических ожиданий.

Вот, пожалуйста, mx плюс y равен mx плюс my.

Теперь математическое ожидание произведения двух и конечного числа случайных величин равно произведению их математических ожиданий.

Вот, пожалуйста.

То есть математическое ожидание произведения двух случайных величин равно произведению их математических ожиданий.

Теперь дисперсия.

Дисперсия или рассеяние дискретной случайной величины

Называется математическое ожидание квадрата отклонения случайной величины от его математического ожидания.

То есть математическим формулой, если записать, вот.

То есть математическое ожидание, пожалуйста, ребята, от квадрата, отклонение – это разность, отклонение самой дискретной величины от его математического ожидания.

Вот, пожалуйста.

Теперь, свойства дисперсии.

Какие свойства эта дисперсия имеет?

Во-первых, дисперсия постоянной величины равно нулю, ребята.

Вот, пожалуйста, запомните.

Математическое ожидание постоянной величины – это само число, а дисперсия равно нулю.

Второе.

Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат, ребята, пожалуйста.

Третье.

Дисперсии суммы конечного числа случайных величин равно сумме их дисперсий.

Вот, пожалуйста.

То есть это свойство работает и для двух, и для n только конечных конечного числа случайных величин.

Бесконечно их взять не можете.

Теорема.

Запомните.

Что хочу я доказать теоремой?

Оказывается, формула, которая дает по определению, по определению понятно, но для вычисления дисперсии она очень неудобная.

Поэтому мы с вами введем формулу для вычисления дисперсии.

Вот, пожалуйста.

Оказывается, дисперсия случайной величины равно разности математического ожидания квадрата случайной величины

и квадрата математического ожидания самой случайной величины.

То есть дисперсия равна разности, как я говорю, математическому ожиданию, квадрата этого х и квадратом ее математического ожидания.

Попробуйте эту формулу доказать, ребята, дома.

Очень просто доказывается.

Если не сможете, в субботу на практическом занятии я вам ее докажу.

Среднее квадратическое отклонение.

Среднее квадратическое отклонение – это квадратный корень из дисперсии, ребята.

Вот, пожалуйста.

Поэтому, запомните, вообще не только поэтому, само определение дисперсии говорит о том, что дисперсия не может быть отрицательным.

И также квадратическое отклонение, так как мы вычисляем квадратный корень из положительного числа.

Вот, пожалуйста.

Теперь, например, вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение дискретно случайной величины х, определяемое как количество студентов наугад в выбранной группе, используя следующие данные.

Вот, пожалуйста.

То есть в выбранной группе 8 учеников 0,2, вероятность 0,2, 0,2 десяток, 9 людей 0,1, 10, 0,3, 11, 0,2, 12, опять 0.

Как вы видите, сумма этих вероятностей 1, 0,3, 0,3, 1.

Значит, сумма 1.

Вот у нас закон распределения.

Мы должны найти математическое ожидание, дисперсию и квадрат.

К средних подратитесь к отклонению.

Математическое ожидание.

Вы должны, вот, х1 на p1 плюс х2 на p2 плюс х3 на p3 и так далее, х5 на p3, 5.

Вот, пожалуйста, 8 на 0, 2, 9 на 0, 1, 10 на 0, 3 и так далее.

Вот наше математическое ожидание.

Теперь попробуем вычислить дисперсию, ребята.

Дисперсия.

По формуле дисперсии вы должны 8 в квадрате умножить на 0,2, плюс 9 в квадрате на 0,1, плюс 10 в квадрате на 0,3, плюс 11 в квадрате на 0,2 и плюс 12 в квадрате на 0,2.

И минус квадрат математического ожидания.

Вот, пожалуйста, то, что я вам сейчас предректовала.

То есть дисперсия у нас равна 1,89.

И если мы из квадратного корня вычислим, среднее квадратическое отклонение у нас будет равно 1,37.

Вот и все.

То есть самое главное, чтобы нам было дано закон распределения, либо задается задача, где надо сначала составить закон распределения, а потом найти его числовые характеристики, ребята.

Так, теперь математическое ожидание и диспетчер числа появления в независимых испытаниях.

Если, запомните,

Вероятность появления события А в каждом испытании постоянная и не зависит от исходов других испытаний, то такие испытания называются независимыми.

Мы рассмотрим, я вам сказала, постоянно, то есть одинаково, но вероятность события А может быть в каждом испытании разными.

В данном случае мы с вами рассмотрим, когда вероятность события А в каждом испытании одинаковая, то есть постоянная.

Тогда математическое ожидание, ну, не, не, вот смотрите, если вероятность то, что А в каждом событии произойдет равно П, а не наступление, это будет Q, ребята, мы с вами это проходили, Q равен 1 минус П, тогда математическое ожидание, смотрите, числа появления события А в N независимых испытаний равно вот так.

То есть я вам еще раз повторяю теорему.

Математическое ожидание числа появления события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события А в каждом из этих испытаний.

Теперь теорема.

Дисперсия числа появления события А в независимых испытаниях равна произведению числа испытаний на вероятности появления и непоявления события А в одном испытании.

Вот, пожалуйста.

То есть дисперсия – это NPQ.

Понятно, ребята?

У меня... А, еще есть...

Теперь, вот в 5 аптеках проверяется годовой баланс.

Вероятность правильного оформления баланса в каждой аптеке равна 0,7.

Найти математическое ожидание дисперсию правильно оформленных балансов.

То есть мы проверяем 5 аптек.

N у меня 5.

Вероятность того, что правильно каждая аптека составляет баланс 0,7, а то, что неправильно 0,3.

Находим MX.

MX это NP.

5 умножим на 0,7.

То есть из половины.

А дисперсия просто умножаете n, p, q. Вот 1,05.

Вопрос ясен, ребята?

Нет.

Почему?

Вот смотрите.

Проверяем 5 аптек.

Вероятность того, что каждая аптека правильно оформляет баланс 0,7, а то, что неправильно, от 1 отнимаю 0,7, то есть 0,3.

Формула я вам дала.

Математическое ожидание равно n умножено p. Вот n 5 аптек, p у нас 0,7.

У меня получается 3,5.

А дисперсия N, P, Q, вот 5N, 5 аптек, 0,7 то, что они правильно оформляют баланс, и 0,3 то, что неправильно, это будет 1,05.